




: 整列:ソート
: リストの処理
: リストに対する基本計算
目次
索引
リストと再帰呼び出し
リストの要素はまたリストでよいという再帰的構造が存在しているので,
リスト処理の関数は, 再帰を用いると気持よく書けることがおおい.
例 12.3 リストの中に、数値データが何個あるかを数える関数
count_numbers を作れ.
たとえば
count_numbers([ 1, cat, 3])
は 2 を戻す.
ただし, リストの中に入る要素は, 数か多項式か文字列かリストに限る
ものとする.
(ヒント:
type を使う. )
データ型をみる関数
type(L)
は
L がリストの時 4,
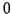
以外の数字のとき 1,
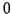
のとき 0 を戻す.
よって次のプログラムでよい.
プログラム
def count_numbers(L) {
if (length(L) == 0) return(0);
C = car(L);
if (type(C) == 0 || type(C) == 1) {
return(1 + count_numbers(cdr(L)));
}else if (type(C) == 4) {
return(count_numbers(C)+count_numbers(cdr(L)));
}else{
return(count_numbers(cdr(L)));
}
}
問題 12.4 リストの中に、リストが何個あるかを数える関数
count_lists を作れ.
たとえば
count_lists([ [0,1], "cat", [[ 7, 8], 3] ])
は 2 を戻す.
問題 12.5
第
8 章の問題の
clone_vector を再帰的に書くことにより,
任意のベクトルの複製を作れるように書き換えよ.
問題 12.6
リスト
L のなかに与えらた要素
A が存在してるかどうか
判定する関数
member(A,L) をかけ.
問題 12.7
Well-formed formula とはたとえば、
[or, p,[and,[[not,p], q]]]
なる形の式だとする. ここで、 p, q
は真(1)または偽(0)だとする.
常に真である式を恒真式という.
与えられた Well-formed formula が恒真式かどうか判定する関数を作れ.
問題 12.8 リストの要素を一列に並べる関数を書け.
という操作を行うという意味である. (
list_append を使ってよい.)
問題 12.9 与えられたリストの要素を並べ変えて得られる全てのリストから
なるリストを返す関数を書け.
たとえば,
[1,2] を入力とした場合は,
[[1,2],[2,1]], それから
[1,2,3] を入力したときは
[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
をもどす関数.
ヒント:
- 与えられたリストを
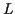 とし, その長さを
とし, その長さを 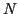 とする.
とする.
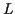 は
は ![$L[0]$](img423.png) から
から ![$L[N-1]$](img424.png) までの要素をもつ.
までの要素をもつ.
- 結果を保持するリスト
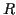 を用意する. 最初は
を用意する. 最初は ![$[]$](img426.png) にしておく.
にしておく.
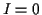 から
から 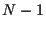 に対して次の操作を行う.
に対して次の操作を行う.
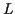 から
から ![$L[I]$](img429.png) を抜いたリストを
を抜いたリストを 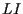 とする.
とする.
(例 ![$L=[1,2,3,4]$](img431.png) から
から ![$L[1]$](img432.png) を抜くと
を抜くと ![$LI=[1,3,4]$](img433.png) )
)
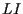 は長さ
は長さ 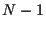 のリストで, これを引数として自分を呼び出し,
のリストで, これを引数として自分を呼び出し,
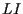 から生成される順列全てのリスト
から生成される順列全てのリスト 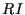 を作る.
を作る. 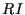 の要素はまたリスト.
の要素はまたリスト.
(上の場合,
![$RI=[[1,3,4],[1,4,3],[3,1,4],[3,4,1],
[4,1,3],[4,3,1]]$](img435.png) .)
.)
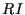 の各要素の先頭に
の各要素の先頭に ![$L[I]$](img429.png) を付け加える.
を付け加える.
(上の場合,
![$[[2,1,3,4],[2,1,4,3],[2,3,1,4],[2,3,4,1], [2,4,1,3],[2,4,3,1]]$](img436.png) となる.)
となる.)
- これを, 結果を保持するリスト
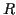 に追加する.
に追加する.
ここでの方法ではリストの 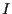 番目を抜く関数が必要となる.
これは, 例えば
重なった
番目を抜く関数が必要となる.
これは, 例えば
重なった 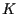 枚の紙があったとして, その上から
枚の紙があったとして, その上から 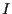 番目の紙を抜き出す
場合を考えればなにをすればよいか分かると思う. くどいのを承知で説明
すると
番目の紙を抜き出す
場合を考えればなにをすればよいか分かると思う. くどいのを承知で説明
すると
- 一番上から 1 枚ずつとって, 順に隣に重ねる操作を
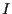 回行う
回行う
- 一番上をはずす. (隣には重ねない.)
- 隣の紙を一枚ずつ順に戻す.
とすればよい.
いずれにしても, 再帰で書くことになるが, 注意すべき点は, 再帰の終点
をどこにするかである. 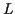 の長さが 1 の場合に終点とすれば分かりやすい.
この場合
の長さが 1 の場合に終点とすれば分かりやすい.
この場合 ![$L=[a]$](img437.png) なら
なら ![$[[a]]$](img438.png) を返すようにすればよい. (結果は
順列 (リスト) のリストとなることに注意.)
を返すようにすればよい. (結果は
順列 (リスト) のリストとなることに注意.) ![$L=[\ ]$](img439.png) を終点とすること
もできるが, この場合
を終点とすること
もできるが, この場合 ![$[[\ ]]$](img440.png) (空リストを要素とするリスト) を返す
必要がある. こうしないと, 再帰が進まない.
(空リストを要素とするリスト) を返す
必要がある. こうしないと, 再帰が進まない.





: 整列:ソート
: リストの処理
: リストに対する基本計算
目次
索引
Nobuki Takayama
平成15年9月12日