2 分法とニュートン法

計算機では整数の四則計算の組み合わせで, より複雑な計算をしているとおもってほぼまちがいない. たとえば $\sqrt{a}$ の近似計算を考えてみよう. この数を近似計算するにはいろいろな方法があるが, 一つの方法は, $\sqrt{a}$は $y = x^2-a$ と $y=0$ の交点をもとめることである. 一般に $f(x)$ を連続微分可能関数とし,

$$y = f(x)$$

と $y=0$ の交点を近似的に求めることを考えてみよう.

点 $x=x_n$ における $y=f(x)$ の接線の方程式は,

$$y-f(x_n) = f'(x_n)(x-x_n)$$

である. したがって, この接線の方程式と $y=0$ との交点は,

$$x_n -f(x_n)/f'(x_n)$$

となる. 数列 $x_k$ を次の漸化式できめよう.

$$x_{k+1} = x_k -f(x_k)/f'(x_k)$$

いま, $f(x)=0$ の根 $r$ に十分近い数 $x_0$ をとり, 上の漸化式で, 数列 $x_k$ を決めていけば, $f'$ が $0$ でない限り, $x_k$ は $r$ に収束していくであろう. これは, 厳密に証明せずとも, 図 6.1 をみれば納得できるであろう. このように $f(x)=0$ の根を求める方法を Newton 法とよぶ. Newton 法は, 出発点とする十分近い解を見付けることが できれば, 非常に収束が早い. しかしながら, やや安定性に欠ける.

図 6.1: Newton 法が収束する例

$\parbox{6cm}{ \scalebox{0.4}{\includegraphics{Figures/stable.ps}}}$

    

図 6.2: Newton 法が収束しない例

$\parbox{6cm}{ \scalebox{0.4}{\includegraphics{Figures/unstable.ps}}}$

たとえば図 6.2 を見られたい. この図は, $f(x)=x^3-3x^2+x+3$ に対し, $x_1=1$ からスタートした Newton 法の挙動を示している. この場合, $x_n$ は 1 と 2 という値を 繰り返しとることになる. これは極端な例だが, 極値の周辺で, 不安定な状況が起こることは容易に想像がつくであろう.

初期値さえ適切ならば, Newton 法は高速に $f(x)=0$ の 解を求めることができる. Newton 法で $\sqrt{x}$ の近似値を求めるプログラムは以下のとおり.

def sqrtByNewton(A) {
  Epsilon = 0.0001;
  P = 0.0;
  Q = deval(A);
  while (!( (Q-P > -Epsilon) &&
            (Q-P < Epsilon))) {
     P = Q;
     print(Q);
     Q = P-(P*P-A)/(2.0*P);
  }
  return(Q);
}

    

たとえば, $\sqrt{2}$ は次のように計算できる.

[422] sqrtByNewton(2);
2
1.5
1.41667
1.41422
1.41421

Newton 法ほど早くないが, 安定性のある方法として, 2 分法 (bisection method) がある.

$f$ が連続関数とするとき, $f(a) < 0$ かつ $f(b) > 0$ なら $f(\alpha) = 0$ となる根 $\alpha$ が 区間 $(a,b)$ に存在するという事実を思いだそう. この事実をもちいて, 根の存在範囲を狭めていくのが, 2 分法である.

def bisection(A,B,F) {
  Epsilon = 0.00001;
  A = deval(A); B=deval(B);
  if (subst(F,x,A) >= 0 || subst(F,x,B) <= 0) 
    error("F(A)<0 and F(B)>0 must hold.");
  while (true) {
    C = (A+B)/2;
    if ((A-B > -Epsilon) && (A-B < Epsilon))
      return(C);
    FC = subst(F,x,C);
    if (FC > 0) B = C;
    else if (FC < 0) A = C;
    else if (FC > -Epsilon && FC < Epsilon)
      return(C);
  }
}

    

左のプログラムでは, 根の存在区間の幅が Epsilon よりも 小さくなった時にループを抜けて, その区間の中点の値を返す. 実行すると次のようになる.

[205] bisection(1,2,x^2-2);
1.41421

問題 6.1   (1) 上のプログラムには解説がほとんどない. プログラムの仕組みを解読して解説せよ. (2) 2 分法で根がもとまる様子を観察できるようにプログラムを改造せよ. Newton 法での収束の様子と比較せよ.

上の問題で, 収束の様子を調べたが, Newton 法でもとまった近似解にどの程度誤差があるかは, 次のようにして理論的に調べることが可能である.

根を $\alpha$, $x_n$ をニュートン法にあらわれる 根の近似値の列, 誤差を

$$\varepsilon_n = x_n - \alpha$$

とおく.

以下, $\varepsilon_{n+1}$ は, $\frac{\varepsilon_n^2}{2}\frac{f''(\alpha)}{f'(\alpha)}$ にほぼ等しいということをテイラー展開を用いて証明する.

$x_n = \alpha+\varepsilon_n$ なので, テイラー展開の公式から, $\alpha < \xi_i < x_n$ を満たす定数 $\xi_i$ が存在して,

$$\begin{eqnarray*} f(x_n) &=& f(\alpha) + \varepsilon_n f'(\alpha) + \frac{\vare... ...psilon_n f''(\alpha) + \frac{\varepsilon_n^2}{2} f'''(\xi_2)\\ \end{eqnarray*}$$

がなりたつ. 定義より,

$$\begin{eqnarray*} \varepsilon_{n+1} &=& x_{n+1} - \alpha \\ &=& x_n - \frac{f(x... ...f'(x_n)} - \alpha \\ &=& \varepsilon_n - \frac{f(x_n)}{f'(x_n)} \end{eqnarray*}$$

がなりたつ. これにテイラー展開の式を代入すると,

$$\begin{eqnarray*} \varepsilon_{n+1} &=& \varepsilon_n - \frac{\varepsilon_n f'... ...repsilon_n f''(\alpha) + \frac{\varepsilon_n^2}{2} f'''(\xi_2)} \end{eqnarray*}$$

最後の式は, 近似的に $\frac{\varepsilon_n^2}{2}\frac{f''(\alpha)}{f'(\alpha)}$ に等しい. $n$ ステップ目での誤差が $\varepsilon_n$ なら $n+1$ ステップ目では誤差が $\varepsilon_n^2$ のオーダーとなる.

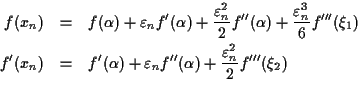
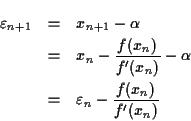
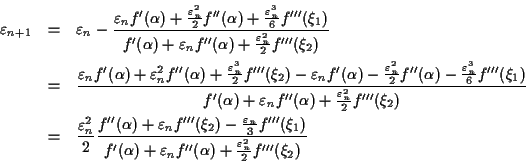
したがって, ニュートン法の誤差は, 2 乗, 4 乗, 8 乗, $\ldots$ と急速に減っていく. たとえば, $f(x) = x^2 -2$ の時, 正の根 $\alpha$ は約 $1.14213$ である. このとき $\frac{f''(\alpha)}{2 f'(\alpha)}$ の値は $-0.177$ である. $\vert x_n-\alpha\vert < 10^{-p}$ なら, ほぼ $\vert x_{n+1}-\alpha\vert < 1.77 \times 10^{-2p}$ となる.

実際, 精度の高い浮動小数点計算を遂行する次のプログラムで, 誤差の様子をプリントすると 以下のようになる.

setprec(20);
def sqrtByNewton(A) {
  Epsilon = (1/10)^20;
  P = 0;
  Q = A;
  while (!( (Q-P > -Epsilon) &&
            (Q-P < Epsilon))) {
     Q=eval(Q*exp(0)); print(Q);
     P = Q;
     Q = P-(P*P-A)/(2*P);
  }
  return(Q);
}

    

出力結果

[431] sqrtByNewton(2)$
2.00000000000000000000000000000000000000
1.500000000000000000000000000000000000000
1.416666666666666666666666666666666666670
1.414215686274509803921568627450980392162
1.414213562374689910626295578890134910125
1.414213562373095048801689623502530243620
[432] eval(2^(1/2));
1.414213562373095048801688724204443084493

関数 setprec で, 何桁の有効数字で計算をおこなうかを指定できる. setprec(n) の $n$ を大きくすると, 高い精度で近似計算をおこなう. sin などの関数の近似値を高い精度で計算するには, 次のように関数 eval を用いる.

eval(sin(@pi/3));

参考: 1 変数代数方程式の解法については, Frisco の 最終報告書の Algorithmic Research/Task 3.4: Numerical solving/ 3.4.1 Univariate solving
http://www.nag.co.uk/Projects/Frisco/frisco/node7.htm にいろいろな方法の比較がある. pari(root, 多項式) は Schoenhage アルゴリズムを用いて根を求めている.