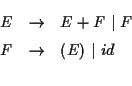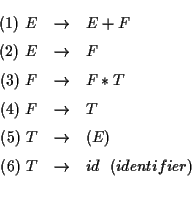
前の節で説明した構文解析の方法を再帰降下法とよぶ. この方法は終端記号, 非終端記号に対応した関数を用意したら, あとは 構文図に従いこれらの関数を呼び出していけばよい.
この方法より効率のよい構文解析の方法が LR パーサである. この話題は上級の話題なので再帰降下で十分という方は読み飛ばされたい.
さて, この節ではこの構文解析法の原理を簡略に説明する. 詳しくは, Aho, Ullman の本 コンパイラを御覧いただきたい [1]. LR パーサではつぎのように構文解析する.
SLR (simple LR) 構文解析法の説明を例を用いて説明する. 次の文法(生成規則)に対するSLR パーサを作ろう. この文法は [1] の 例 6.1 でとりあげられている文法である.
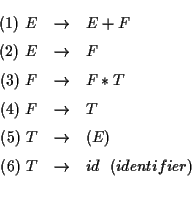
これは
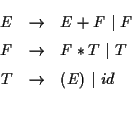
E は expression, F は factor, T は term の略である.
id (identifier) は数である.
したがって,
![]() とか
とか
![]() とかは
この文法をみたしている.
なお
とかは
この文法をみたしている.
なお![]() は満たしていないことを注意しておく.
は満たしていないことを注意しておく.
SLR 法では文法より次のような構文解析表をつくって それを用いたオートマトンで構文解析をする.
| 状態 | id | + | * | ( | ) | ; | E | T | F |
| 0 | s5 | s4 | s1 | s2 | s3 | ||||
| 1 | s6 | OK | |||||||
| 2 | r2 | s7 | r2 | r2 | |||||
| 3 | r4 | f4 | r4 | r4 | |||||
| 4 | s5 | s4 | s8 | s2 | s3 | ||||
| 5 | r6 | r6 | r6 | r6 | |||||
| 6 | s5 | s4 | s9 | s3 | |||||
| 7 | s5 | s4 | s10 | ||||||
| 8 | s6 | s11 | |||||||
| 9 | r1 | s7 | r1 | r1 | |||||
| 10 | r1 | s7 | r1 | r1 | |||||
| 11 | r5 | r5 | r5 | r5 |
この構文解析表をもちいてどの様に構文解析をやるか 説明しよう. エラーの処理とOK(受理)の処理は省略してある.
driver:=
00: push(0); (* 状態0をスタックへ積んで置く.*)
01: c = ipop();
02: state = peek();
03: action = actionTable[state,c];
04: If action == 移動(s) then
05: push(c);
06: push(nextStateTable[state,c]);
07: else (* 還元する. *)
08: rule = nextStateTable(state,c);
09: rule 分 pop() する;
10: ipush(c);
11: ipush( rule の左辺 );
12: endif
14: Goto[1];
各関数の働きはいかのとおり.
03: を終了した時点での各変数の様子を次の入力データ 2+3*5; に対して見てみよう.
c state action stack, inputStack
s {
} , { +,3,*,5,; }
+r {
}, { 3,*,5,; }
Fs {
}, { +,3,*,4,; }
次にどの様にして文法より構文解析表を作るのか説明しよう. 状態の集合, nextStateTable および Following[非終端記号]の 三つのデータを計算すれば構文解析表ができる.
まず, 状態の集合の計算法を示そう.
生成規則の右辺に ![]() を含む生成規則を項 (item) とよぶ.
たとえば生成規則
を含む生成規則を項 (item) とよぶ.
たとえば生成規則
![]() を項とする. Closure(I) とは
を項とする. Closure(I) とは![]() を含む項の集合であり,
次の性質を満たすものとする.
を含む項の集合であり,
次の性質を満たすものとする.
たとえば
![]() の Closure を計算すると
の Closure を計算すると
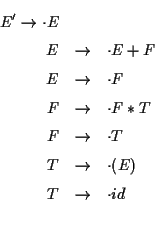
状態 ![]() が項
が項
例として,
nextStateTable[ ![]() ,
, ![]() ]
を計算してみよう.
]
を計算してみよう.
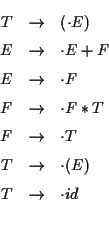
状態 ![]() が
が
状態 ![]() が
が