Execute Loadall to load packages before executing examples.
Dx means ![]() .
.
[ [( (x Dx)^2 + (y Dy)^2 -1) ( x y Dx Dy -1)] (x,y)
[ [ (Dx) 1 (Dy) 1] ] ] gb pmat ;
Output:
[ [ x^2*Dx^2+y^2*Dy^2+x*Dx+y*Dy-1 , x*y*Dx*Dy-1 , y^3*Dy^3+3*y^2*Dy^2+x*Dx ] [ x^2*Dx^2+y^2*Dy^2 , x*y*Dx*Dy , y^3*Dy^3 ] ]The first line is the Gröbner basis and the second line is a set of generators of the initial ideal with respect to the weight vector
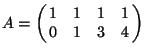 and
and [ [[1 1 1 1] [0 1 3 4]] [1 2]] gkz ::Output:
[ x1*Dx1+x2*Dx2+x3*Dx3+x4*Dx4-1 , x2*Dx2+3*x3*Dx3+4*x4*Dx4-2 , Dx2*Dx3-Dx1*Dx4 , -Dx1*Dx3^2+Dx2^2*Dx4 , Dx2^3-Dx1^2*Dx3 , -Dx3^3+Dx2*Dx4^2 ]
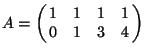 and
and
{ [ [[1 1 1 1] [0 1 3 4]] [1 2]] gkz rrank ::} timer
{ [ [[1 1 1 1] [0 1 3 4]] [0 0]] gkz rrank ::} timer
Output:
5 User time: 1.000000 seconds, System time: 0.010000 seconds, Real time: 1 s 4 User time: 1.320000 seconds, System time: 0.000000 seconds, Real time: 1 s
(oxasir.sm1) run [(x^3 - y^2 z^2) (x,y,z)] annfs /ff set ff message ff 1 get 1 get fctr ::Output:
[ [ -y*Dy+z*Dz , 2*x*Dx+3*y*Dy+6 , -2*y*z^2*Dx-3*x^2*Dy , -2*y^2*z*Dx-3*x^2*Dz , -2*z^3*Dx*Dz-3*x^2*Dy^2-2*z^2*Dx ] , [-1,-139968*s^7-1119744*s^6-3802464*s^5-7107264*s^4-7898796*s^3-5220720*s^2-1900500*s-294000]] [[ -12 , 1 ] , [ s+1 , 1 ], [3*s+5 , 1], [ 3*s+4, 1], [6*s+7, 2], [6*s+5, 2]]The first two rows of the output give generators of the annihilating ideal of
(cohom.sm1) run
[(x^3-y^2) (x,y)] deRham ;
Output:
0-th cohomology: [ 0 , [ ] ] -1-th cohomology: [ 1 , [ ] ] -2-th cohomology: [ 1 , [ ] ] [1 , 1 , 0 ]This means that
(cohom.sm1) run [ [(Dt - (3 t^2-x)) (Dx + t)] [(t)] [ [(t) (x)] [ ]] 0] integrationOutput:
[ [ 1 , [ 3*Dx^2-x ] ] ]