Computing syzygies

Let $R$ be a ring and $f_1, \ldots, f_m$ be elements of $R$. The left $R$-module

$$\{ (s_1, \ldots, s_m \in R^m \,\vert\, \sum_{i=1}^m s_i f_i = 0 \}$$

is called the syzygy among $f_1, \ldots, f_m$. The following script computes the generators of the syzygy among

$$x \partial_{x} + y \partial_{y} , \partial_{x} ^2 + \partial_{y} ^2$$

in the homogenized Weyl algebra.

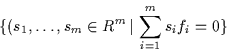
%% syz.sm1

[ (x,y) ring_of_differential_operators
  [[(Dx) 1 (Dy) 1]] weight_vector
 0
] define_ring

[ (x Dx + y Dy).
  (Dx^2 + Dy^2).
] /ff set

ff { [[(h). (1).]] replace homogenize} map /ff2 set

[ff2 [(needBack) (needSyz)]] groebner /ans set ;
(Syzygies are ...) message
ans 2 get ::

The 0-th element of ans is the Gröbner basis. The 1st element of ans is the transformation matrix from the input to the Gröbner basis. The 2nd element of ans is a set of generators of the syzygies of the input.